Excel ရဲ့ FV function (Future Value) ငွေချေးတာ ငွေစုတာတွေမှာ စမတည် တန်ဖိုး၊ အတိုးနှုန်း၊ ချေးငွေ/စုငွေကာလ သက်တမ်း၊ လစဉ်ပေးသွင်းငွေ စတာတွေ ထည့်ပေးလိုက်ရင် သတ်မှတ်ကာလ အပြီးမှာ စုစုပေါင်း ရှိမဲ့ငွေအရင်းအနှီး၊ ပေးသွင်းရမဲ့ ချေးငွေ တို့ကို တွက်ပေးပါတယ်။
Formula : FV(rate, nper, payment, [pv],[type])
- rate : နှစ်စဉ်အတိုးနှုန်း
- nper : ငွေချေးသက်တမ်း သို့ စုငွေကာလ နှစ်
- payment : လစဉ် ထည့်သွင်း သို့ ပြန်ဆပ်ငွေ
- pv : ချေးငွေ ပမာဏ သို့ စုငွေ ပမာဏ
- type : အတိုးကို လကုန် တွက် မယ်ဆိုရင် 0 ပေးပြီး လဆန်းတွက်မယ်ဆိုရင် 1 ကို ပေးရပါမယ်။
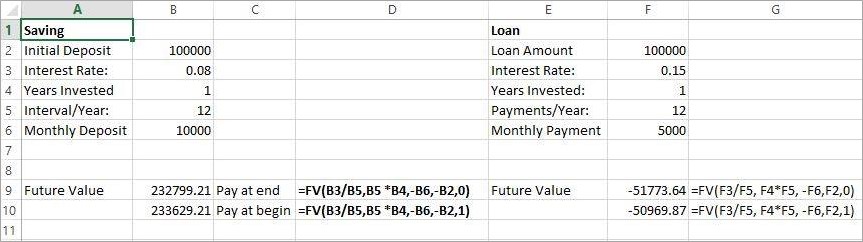
Example : စုငွေ တနှစ်စာ အတိုးနှုန်း 0.08 နဲ့ 100000 စတင်စုပါမယ်။ စုငွေ သက်တမ်းက တစ်နှစ်သတ်မှတ်ပြီး ကြည့်မှာ ဖြစ်တဲ့အတွက် 12 ဖြစ်ပါတယ်။ လစဉ် ပေးသွင်းငွေ က 10000 ဖြစ် တနှစ်ကြာပြီးတဲ့ အချိန်မှာ စုငွေ စုစုပေါင်း ဘယ်လောက် ဖြစ်မယ်ဆိုတာကို FV Function မှာ ထည့်ကြည့်ပါမယ်။ တကယ်လို့ လစဉ်ပေးသွင်းငွေကို လကုန်ရက်မှာ သွင်းမယ်ဆိုရင် တစ်နှစ်ပြီးတဲ့အခါမှာ စုငွေ စုစုပေါင်းက 232799.21 ဖြစ်ပြီး လဆန်းမှာ ပေးသွင်းမယ်ဆိုရင်တော့ လက်ကျန်ငွေက 233629.21 အဖြေထွက်ပါတယ်။
လကုန်ရက် ငွေပေးသွင်းပုံစံ - FV(0.08, 12, 10000 , 100000, 1)
လဆန်းရက် ငွေပေးသွင်းပုံစံ - FV(0.08, 12, 10000 , 100000, ၀)
Example : ချေးငွေ တနှစ်စာ အတိုးနှုန်း 0.15 နဲ့ 100000 ချေးပါမယ်။ ချေးငွေ သက်တမ်းက တစ်နှစ်သတ်မှတ်ပြီး ကြည့်မှာ ဖြစ်တဲ့အတွက် 12 ဖြစ်ပါတယ်။ လစဉ် ပြန်ဆပ် က 5000 ဖြစ် တနှစ်ကြာပြီးတဲ့ အချိန်မှာ လက်ကျန်ချေးငွေ စုစုပေါင်း ဘယ်လောက် ဖြစ်မယ်ဆိုတာကို FV Function မှာ ထည့်ကြည့်ပါမယ်။ တကယ်လို့ လစဉ်ပြန်ဆပ်ငွေကို လကုန်ရက်မှာ ပေးမယ်ဆိုရင် တစ်နှစ်ပြီးတဲ့အခါမှာ စုငွေ စုစုပေါင်းချေးငွေလက်ကျန် က -51773.64 ဖြစ်ပြီး လဆန်းမှာ ပေးမယ်ဆိုရင်တော့ လက်ကျန်ငွေက-50969.87 အဖြေထွက်ပါတယ်။
လကုန်ရက် ငွေပေးသွင်းပုံစံ - FV(0.15 , 12, 5000 , 100000, 1)
လဆန်းရက် ငွေပေးသွင်းပုံစံ - FV(0.15 , 12, 5000 , 100000, ၀)
FV function is the Excel Financial function and it will return the value of an investment or loan at some point in the future.
Formula FV(rate, nper, payment, [pv],[type])
- rate : annual interest rate
- nper : years invested or loaned
- payment : monthly contribution/ deposit pv : principal/initial value
- type : 0 stands to calculate the interest at the of the month and 1 stands to calculate the interest at the beginning of the month.
Example : Saving First initial deposit 100000 is the present value. The interest rate is 0.08 for an annual year. The interest will be added for each month within a year so, the interval/year is 12. Monthly contribution (monthly deposit) is 10000. The objective is to calculate the total saving in hand after 1 year period. (years invested is 1)
- If the deposit is made at the end of month, saving amount in hand will be 232799.21.
- If the deposit is made at the beginning of month, saving amount in hand will be 233629.21.
Example : Loan The loaned value is 100000 as present value. The interest rate for the loan is 0.15 for an annual year. The interest will be added for each month within a year so, the interval/year is 12. The monthly contribution (payment) is 5000. The objective is to calculate the total loan amount left to pay after 1 year period. (years invested is 1).
- If the payment is made at the end of the month, the loan value left in hand will be -51773.64.
- If the payment is made at the beginning of the month, the loan value left in hand is -50969.87